4. Finding motifs¶
(c) 2019 Justin Bois and Michael Elowitz, except for images taken from sources where cited. This work is licensed under a Creative Commons Attribution License CC-BY 4.0. All code contained herein is licensed under an MIT license.
This document was prepared at Caltech with financial support from the Donna and Benjamin M. Rosen Bioengineering Center.

This lesson was generated from a Jupyter notebook. Click the links below for other versions of this lesson.
Design principles¶
- Larger circuits can be understood in terms of recurring functional modules.
- Searching for such motifs can help identify these modules.
Key concepts¶
- Circuit motifs can be identified by comparing the graphs of actual circuits with randomized ensembles of statistically similar circuits.
Techniques¶
- Graph theory approaches
Circuit motifs¶
A regulatory circuit can be thought of abstractly as a directed graph--a set of nodes and arrows connecting them. For the transcriptional circuitry of a bacterium, each node could represent an operon, and each arrow could represent regulation of one operon (tip of the arrow) by a transcription factor in another operon (base of the arrow).
A circuit motif (or ‘network motif’) is defined as an over-represented regulatory pattern--or sub-graph within the overall circuit or graph. To be a 'motif', and not just a pattern, it should occur significantly more frequently than one would expect under some reasonable null hypothesis.
The reason we care about motifs is that their elevated frequency suggests that they have been selected by evolution, perhaps because of their ability to perform important functions within the circuit.
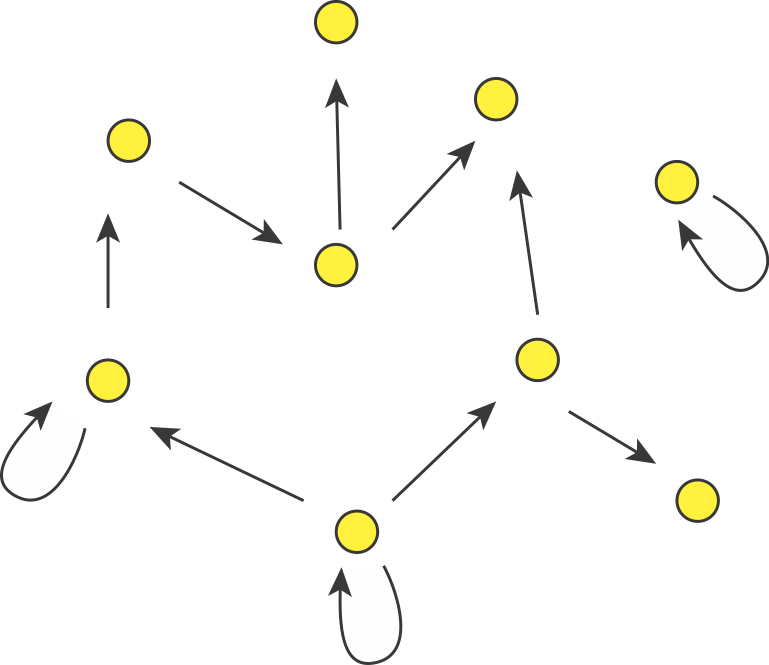
In the last lesson, we briefly introduced this principle in the context of single-gene autoregulation.
We noted:
- E. coli has ≈424 operons, and ≈519 transcriptional regulatory interactions (“arrows”)
- We only expect about one autoregulatory arrow “by chance,” assuing a given arrow selects its target operon randomly.
- However, we observe ≈40 _auto_regulatory arrows (32 negative, 8 positive)
- Autoregulation seems to be over-represented, and is therefore a “motif.” This suggests that it might provide a useful function.
- To think about that funtion might be, we analyzed the dynamics of negative and positive autoregulatory circuits. We found that negative autoregulation accelerates turn-on times, and positive autoregulation, when coupled with ultrasensitivity, can generate bistability.
Today we will try to develop this approach in more detail and apply it to larger motifs, involving 3 genes.
Note: this lecture is based on Alon, Introduction to Systems Biology, Chapter 6
Random graphs enable motif identification¶
Consider a directed graph representing a hypothetical regulatory circuit (left). To find over-represented patterns in this graph, we can compare it to an ensemble of randomized variants and look for sub-graphs that occur more frequently in this circuit than in most of the variants.
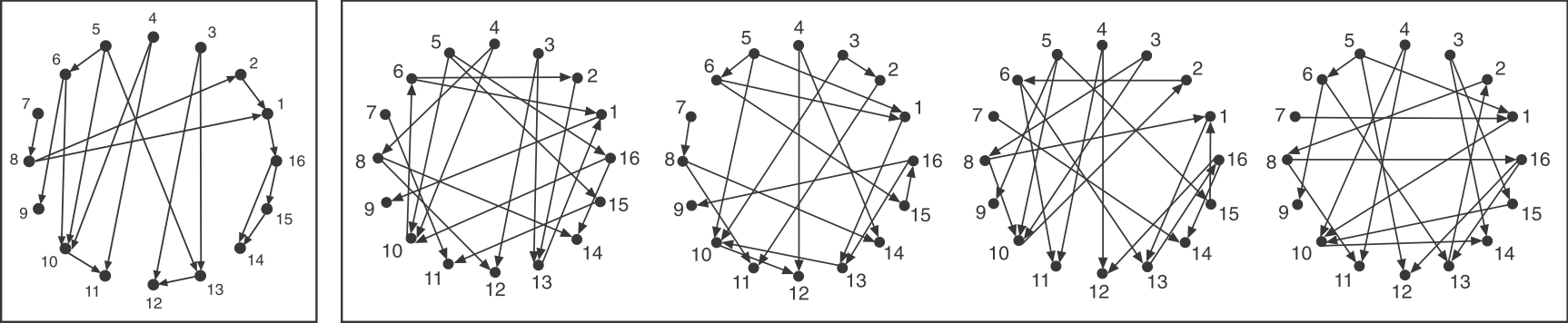
Schematic comparison between a specific circuit (left) and a set of randomized variants with the same incoming and outgoing arrow distributions (right). Image modified from Milo et al, Science, 2002.
To make the comparison as fair as possible, we need to design variant graphs that maintain the key statistical properties of the original graph. Specifically, we insist that all variant graphs have the same number of nodes and arrows. But this is not really enough: It wouldn't make sense to compare this graph, whose arrows are distributed over all the nodes to a variant in which, say, all arrows stem from a single source node, or converge on a single target node. Therefore, we also need to impose a stronger constraint: maintaining the exact distribution of incoming and outgoing arrows for each node.
If you examine the graphs above, you can see that they were constructed to have the same numbered nodes. Furthermore, the number of arrows exiting and entering each numbered node is exactly the same in all graphs. For example, node 4 always has 2 outgoing arrows. Node 6 always has one incoming and two outgoing arrows, node 12 always has 2 incoming arrows, and so on.
To generate the randomized graphs, imagine cutting each arrow in half with a scissors to generate a dangling "+" end connected to an arrowhead and a dangling "-" end connected to a source node. Then one would tie each "+" end to a randomly chosen "-" end. Voila, a new randomized graph is guaranteed, through this procedure, to maintain the same joint distribution of incoming and outgoing arrows. For more details, see the algorithms in Shen-Orr et al, Nat. Genet. (2002) and in M. E. J. Newman et al, Phys. Rev. E (2001).
To implement this type of algorithm, as described in Milo et al, Science, 2002, it is useful to represent the directed graph as a binary non-symmetric square matrix, $\mathsf{M}$. An example of a matrix representation of a graph is shown below. Here, an arrow from node $i$ to node $j$ is represented by $M_{i,j}=1$. The absence of such an arrow would be represented by $M_{i,j}=0$. With this algorithm, one can generate a large ensemble of randomized graphs. Then, one can ask which sub-graphs are significantly more (or less) prevalent in the actual graph than in the randomized variant graphs.

Different views of the same graph, using dots and arrows (left) or as a binary matrix, shown either with 0s and 1s or in black and white (right).
Questions:
- What algorithm would you use to generate the randomized graphs (matrices)?
- How would you control for the bias of smaller motifs in the frequency of larger motifs?
Note: Supplementary information from Milo et al, Science, 2002 here.
Finding 3-node motifs¶
Let's focus on 3-node sub-graphs. These are big enough to be quite interesting, but small enough to be easily conceptualized. There are 13 possible 3-node graphs that exclude direct autoregulation, which are shown here in a drawing from the Alon book:
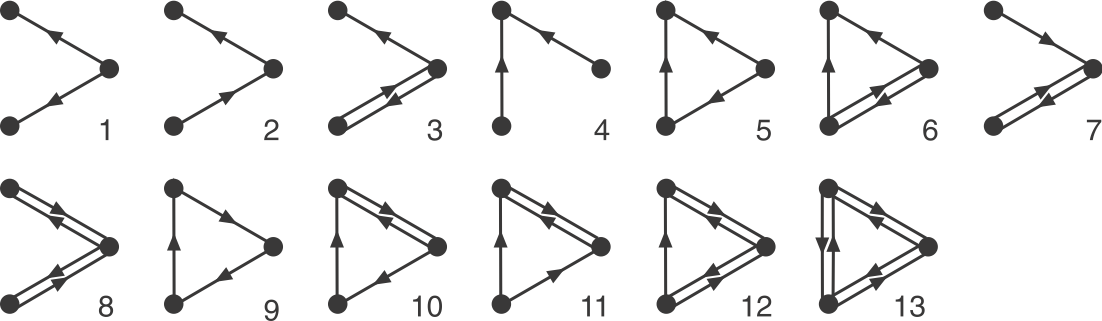
_Image: Alon, U., Introduction to Systems Biology_ Now look back at the schematic graph above. Can you tell which of these sub-graphs are over-represented? The original graphs was constructed to contain a preponderance of one particular sub-graph:
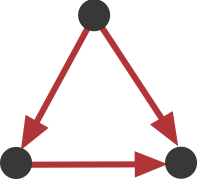
This sub-graph, termed the **Feed-Forward Loop (FFL)**, has one node that regulates a target node two ways: directly, and indirectly through the third node. To visualize this, we can highlight in red all of the FFLs in the graphs shown above:
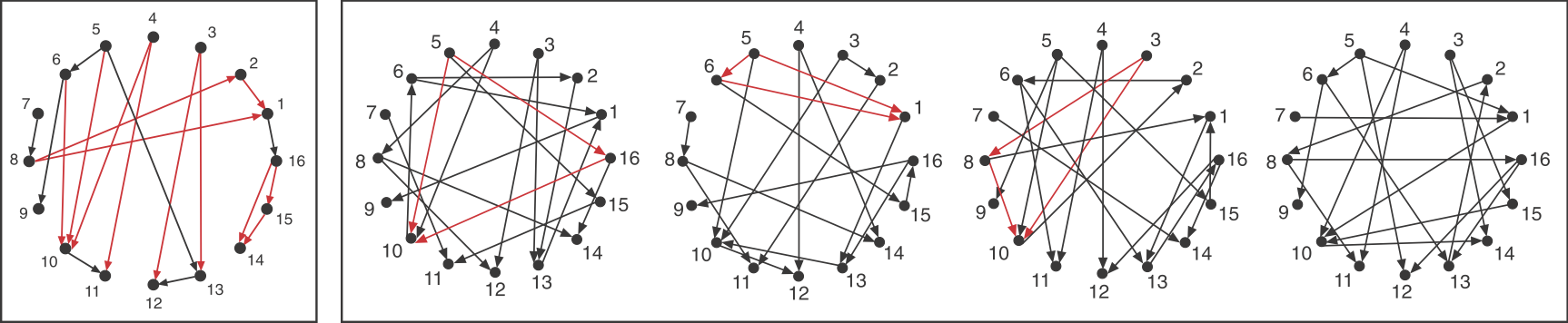
We see that this motif is over-represented. Of course, this is a schematic graph deliberately constructed to illustrate over-representation of this motif. What happens in real circuits? To address this question, Alon & colleagues went through the _E. coli_ transcriptional circuit, and systematically counted how many times they observed each of the 13 sub-graphs shown above. For each one, they compared the number of observations in the real circuit to the distribution of the number of times that sub-graph was observed in a large ensemble of randomized circuits. They used a **Z-score** to quantify over- or under-representation in units of the standard deviation of the number of occurrences for the sub-graph in the randomized circuits: $z = \frac{n_{obs}-
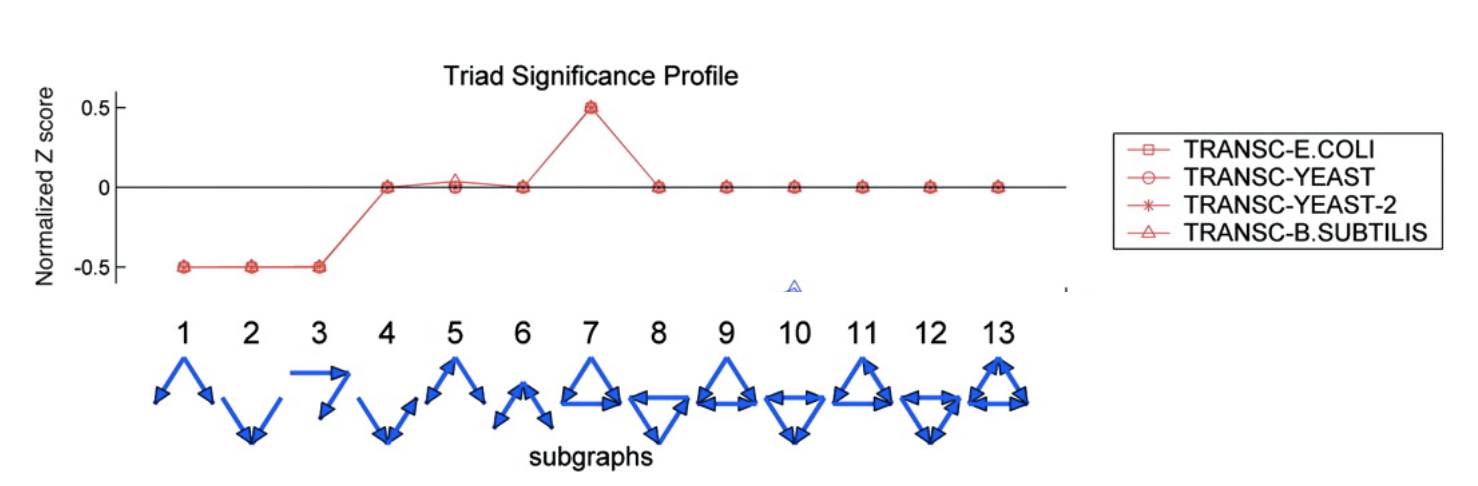
Several features are striking in this plot:
- There is strong over-representation of FFLs. In E. coli, one expects to see 7±5 FFLs by chance, but one observes this pattern 42 times in the real circuit.
- The over-representation of FFLs is strikingly conserved across three distinct organisms, suggesting it is a general property of transcriptional circuits.
- Most sub-graphs are neither over- nor under-represented.
- Three sub-graphs are statistically under-represented. They occur significantly less often than one would expect by chance, provoking the question of what problems they might present as components of larger circuits. These three sub-graphs are all sub-graphs of the FFL sub-graph. Thus, it's not that divergent regulation (sub-graph 1) is rare, it's just that when it does occur, it does so in the context of the FFL.
Aside: sequence motifs identify cis-regulatory sites¶
The motif principle is quite general. Before it was applied to network motifs, it was used to identify functional motifs in genome sequences. For example, Bussemaker et al, PNAS, 2000 presented an algorithm called MobyDick that identifies "words" (letter sequence motifs), in any "text" (sequence of letters). They test it out on the text of the classic novel Moby Dick, with spaces and punctuation removed, recovering English words. Then, they use it on the yeast genome sequence to identify cis-regulatory sites, including transcription factor binding sites.
How do sub-graph abundances scale?¶
However, before we get to this question, let's think a little more deeply about our expectations for sub-graph distributions, using random graphs.
What is the probability of obtaining an n-vertex sub-graph, $G$, by chance in a large random graph with $N$ nodes and $E$ edges? Clearly it will depend on the number of nodes, $n$, and edges, $g$, in $G$. For the FFL, $n=3, g=3$.
Many biological networks are sparse, meaning the probability, $p$, of any potential edge occurring is low. Since the number of possible edges is $N^2$, so that $p = E/N^2 \ll 1$. For E. coli, $p≈0.002$. We will therefore focus on this regime.
The question is: for large sparse graphs, how should the expected number of occurrences of sub-graph, $G$, scale with the size of the circuit, or number of nodes, $N$?. For this argument, we will ignore numerical prefactors, and focus only on the dependence on $N$.
- Within the overall network the number of potential instances of $G$ is the binomial coefficient $\binom{N}{n}$, where $n$ is the number of nodes in $G$, e.g. $n=3$ for the FFL.
- The probability that any one of these potential instances is the desired sub-graph, is proportional to $p^g$, where $g$ denotes the number of edges in the $G$, e.g. $g=3$ for the FFL. There is also a permutation factor, representing the number of different ways that you could make the desired sub-graph from a set of 3 nodes. We neglect this factor because it is independent of $N$.
- Since $N \gg n$, we can use a well-known approximation of the binomial coefficient: \begin{align} \phantom{blah} \\ \binom{N}{n} \approx \frac{N^n e^n}{\sqrt{2\pi} n^{n+1/2}}\\[1em] \phantom{blah} \end{align} This is $N^n$ times numerical factors that are independent of $N$.
- Thus, the expected number of occurrences scales as $N^n p^g$.
- Rewriting this expression provides more insight into the scaling of sub-graph abundance: \begin{align} &\phantom{blah} \\ N_G & \sim N^n p^g \\[1em] &= N^n \left( \frac{E}{N^2} \right)^g \\[1em] &= N^{n-2g} E^g \\[1em] &= N^{n-g} \left( \frac{E}{N} \right)^g\\[1em] \phantom{blah} \end{align} The thing to notice here is that the N-dependence can be captured by an extensive term that scales as $N^{n-g}$ times a function fo the graph's mean connectivity, $E/N$, which is an intensive (N-independent) property.
This result leads to interesting and counterintuitive expectations:
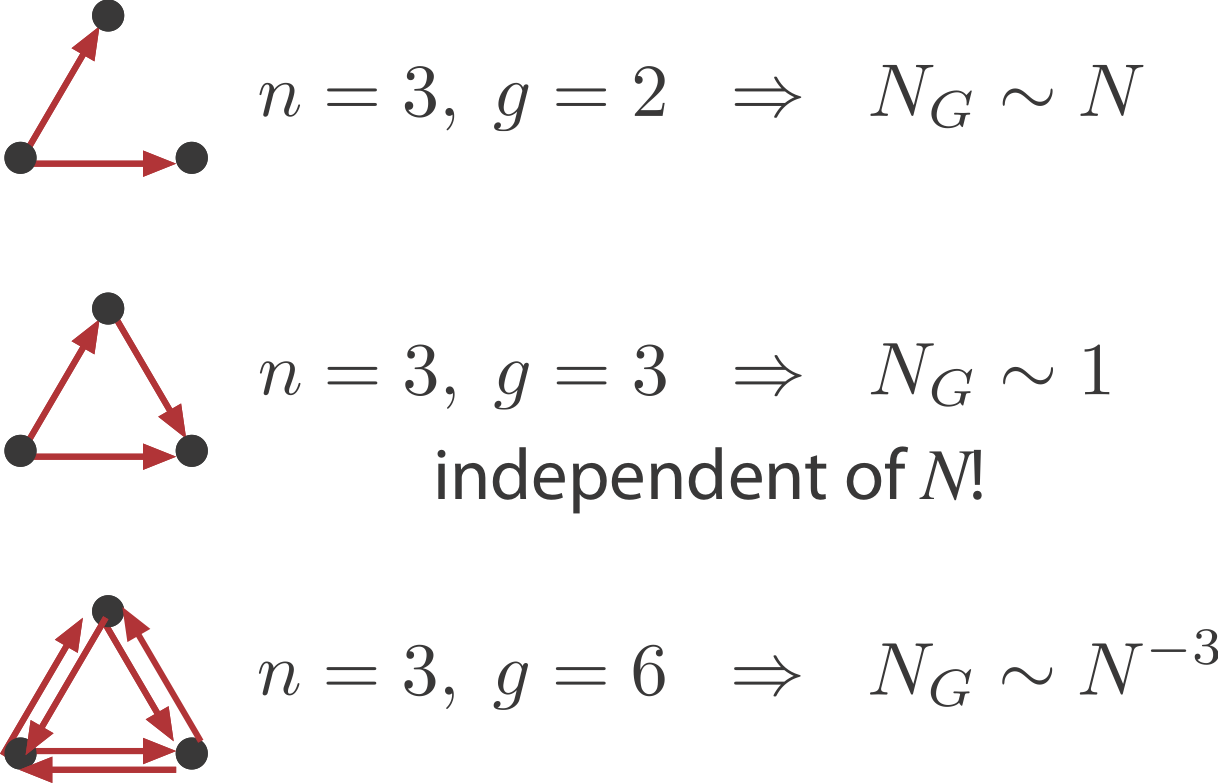
- Sparsely connected sub-graphs increase in frequency with $N$
- Densely connected sub-graphs decrease in frequency with $N$. This means that as the graph grows larger there are actually fewer of these motifs.
- And in between, sub-graphs with the same number of nodes and edges, such as the FFL, actually have a constant expected number regardless of $N$.
Beyond transcriptional circuits¶
It's important to remember that these are expectations for (a particular class of) random networks. Real networks will of course differ, because they are designed, or evolved, to perform specific functions. In fact, different types of systems seem to show quite distinct motif profiles:
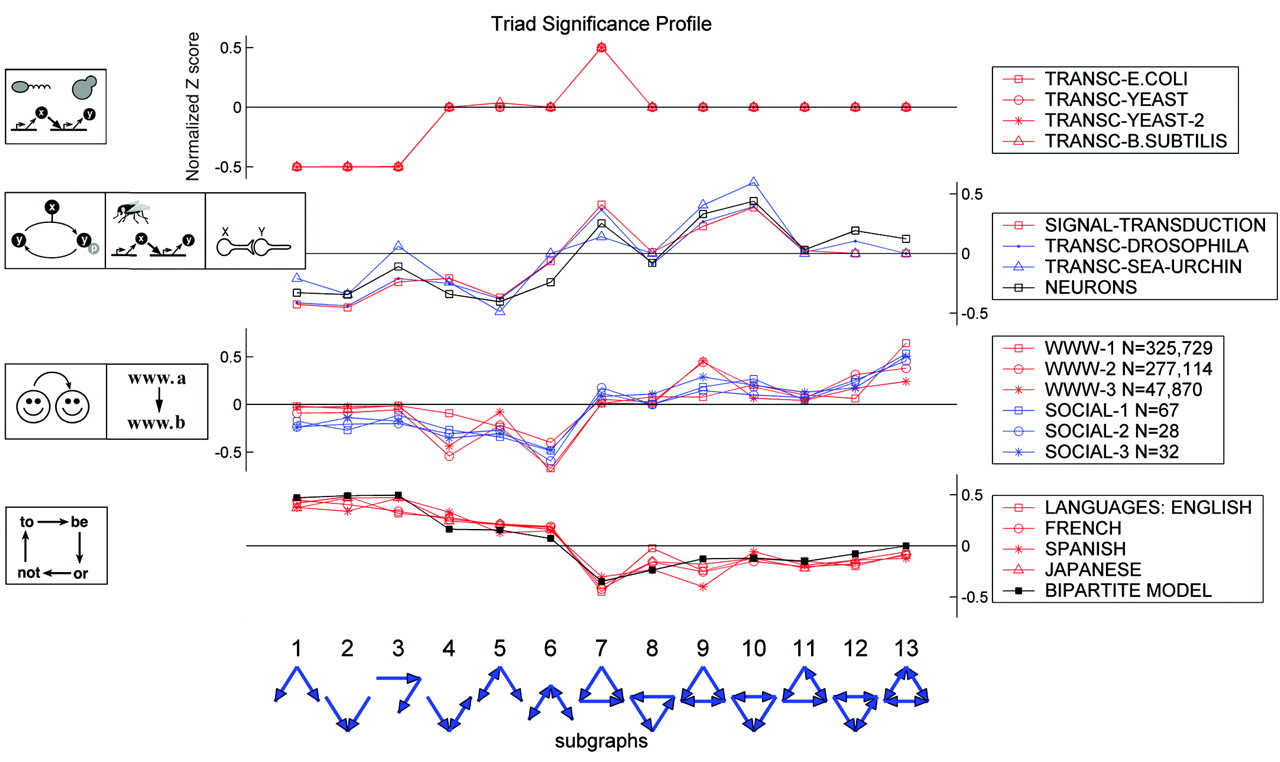
Here, the top group are the transcriptional circuits we already saw. The next group are biological signal transduction circuits of different types from different species. The third group are networks like the world-wide web, for which a directed edge indicates a link from one web page to another. Finally, the lowest group represents motifs in language graphs, in which nodes are words and edges are derived from the probability that one word follows another.
There are many kinds of FFLs¶
Our description of regulatory interactions so far has been oversimplified in a number of ways. We have collapsed positive and negative regulation together. We have not considered how multiple regulators combine to control expression of a mutual target operon. And we have ignored the quantitative strength of the regulation. Trying to understand the function of a motif requires thinking about these aspects more carefully.
We can classify the overall FFL motif into $2^3=8$ different categories depending on which if its 3 arrows are positive or negative:
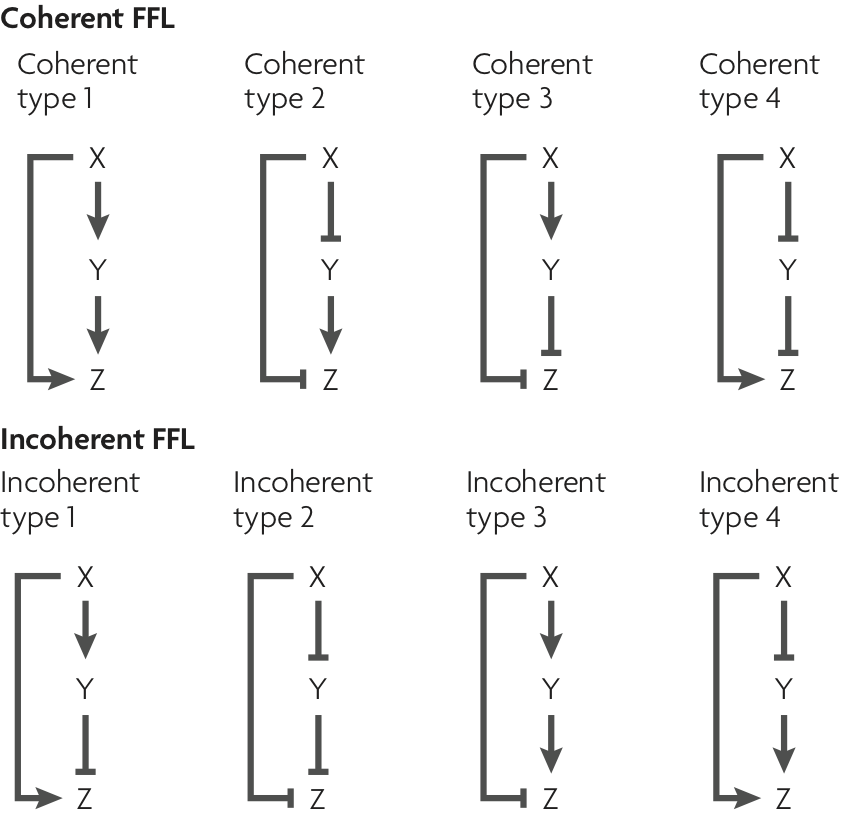
We can then further classify the FFLS, according to how the regulatory arrows converging on the third node (now labeled "Z") combine. In AND regulation, both X and Y need to be simultaneously present at high levels for Z to be expressed. in OR regulation, either input is sufficient to activate Z.
In the next lecture, we will consider what functions the various FFLs can perform for cells.
Summary¶
- Motifs are statistically over-represented patterns in a circuit.
- To find motifs, we construct ensembles of random circuits with the same arrow distributions for comparison.
- The abundances of different sub-graphs can scale in opposite and even counter-intuitive ways as the size of the overall circuit grows
- This approach can be applied to a wide variety of systems that can be represented as graphs.
- Transcriptional regulatory circuits appear to have a single major motif: the feed-forward loop, which can appear in multiple types.
For those who have not previously read it, here is the first paragraph of Moby Dick:
Call me Ishmael. Some years ago - never mind how long precisely - having little or no money in my purse, and nothing particular to interest me on shore, I thought I would sail about a little and see the watery part of the world. It is a way I have of driving off the spleen and regulating the circulation. Whenever I find myself growing grim about the mouth; whenever it is a damp, drizzly November in my soul; whenever I find myself involuntarily pausing before coffin warehouses, and bringing up the rear of every funeral I meet; and especially whenever my hypos get such an upper hand of me, that it requires a strong moral principle to prevent me from deliberately stepping into the street, and methodically knocking people's hats off - then, I account it high time to get to sea as soon as I can. This is my substitute for pistol and ball. With a philosophical flourish Cato throws himself upon his sword; I quietly take to the ship. There is nothing surprising in this. If they but knew it, almost all men in their degree, some time or other, cherish very nearly the same feelings towards the ocean with me.