Homework 1¶
(c) 2019 Justin Bois and Michael Elowitz. With the exception of pasted graphics, where the source is noted, this work is licensed under a Creative Commons Attribution License CC-BY 4.0. All code contained herein is licensed under an MIT license.
This document was prepared at Caltech with financial support from the Donna and Benjamin M. Rosen Bioengineering Center.

This homework was generated from a Jupyter notebook. You can download the notebook here.
1.1: Negative autoregulation, 70 pts¶
Consider the two simple circuits shown below (adapted from Del Vecchio and Murray, Biomolecular Feedback Systems, Figure 2.7), where A is an arbitrary repressor (it could be, e.g., LacI).
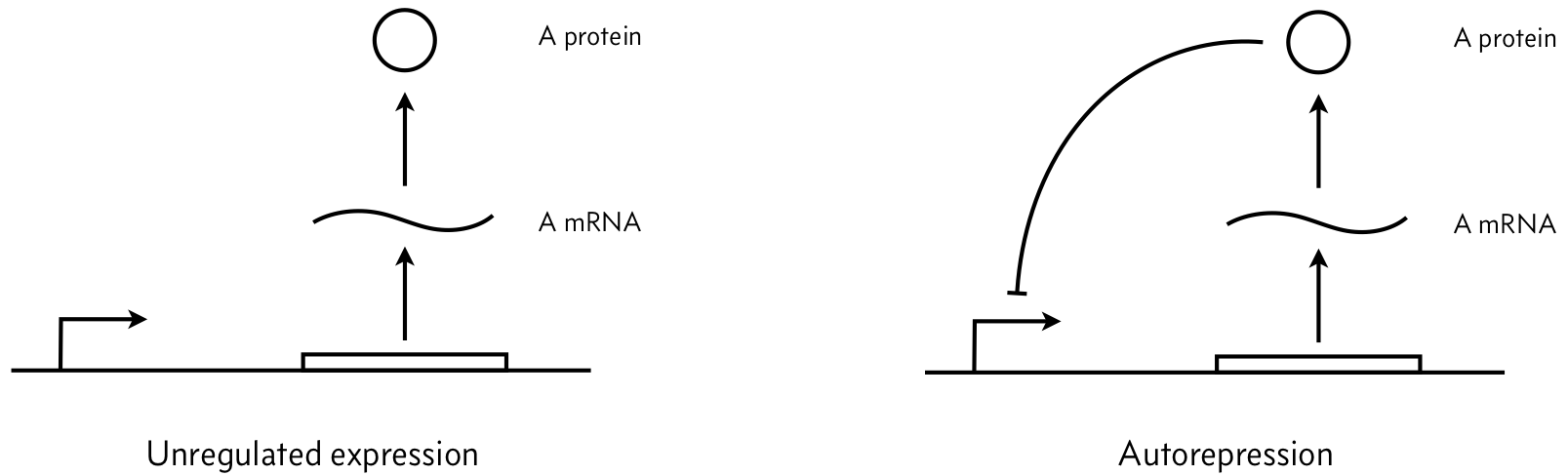
We parametrize the dynamics as follows. Let $\beta_m$ be the unregulated mRNA production rate, $\gamma_m$ be the mRNA degradation rate constant, $\beta_p$ be the protein production rate constant, and $\gamma_p$ be the protein degradation rate constant.
a) Assuming mass action kinetics, write down mathematical expressions in the form of a system of coupled ODEs for the left figure (unregulated expression). Assume that this system exhibits no leakiness.
b) Find the steady state mRNA concentration, $m_0$, and the steady state protein concentration, $p_0$, in terms of the given parameters.
c) Now write down mathematical expressions in the form of a system of coupled ODEs for the right figure (negatively autoregulated expression). Assume that repression serves to decrease the mRNA production rate by a factor of $1/(1 + (p/k)^n)$, where $p$ is the protein concentration. This is a repressive Hill function with Hill coefficient $n$ and activation constant $k$. Again, assume that this system exhibits no leakiness.
d) Define the following dimensionless variables and parameters.
\begin{align} \tilde{t} &= \gamma_m t \\[1em] \tilde{p} &= p/p_0, \\[1em] \tilde{m} &= m/m_0, \\[1em] \gamma &= \gamma_p/\gamma_m, \\[1em] \kappa &= \frac{\gamma_m\gamma_p k}{\beta_m \beta_p}. \end{align}Here, $m$ is the mRNA concentration and $p_0$ and $m_0$ are the steady states found in part (a). Using these expressions rewrite your ODEs from parts (a) and (c) in dimensionless form. You will see that the dynamics for the unregulated circuit depend only on $\gamma$, and those of the regulated circuit depend only on $\gamma$, $\kappa$, and $n$. Comment on the physical meaning of these three dimensionless parameters.
e) One of the ways we quantify the separation of time scales we mentioned in lecture is by evaluating the ratio $\gamma$. Provide an argument why we may neglect the mRNA dynamics and consider only the protein if $\gamma \ll 1$.
f) Assume we initially have no mRNA or protein present. Suddenly, a cell needs to start producing the protein, so the gene is turned on at time $t = 0$. Starting from initial conditions of $m(0) = p(0) = 0$, solve the ODEs (numerically or otherwise) for both the unregulated and autoregulated systems. You should choose parameters as would be typical for a bacterial cell. The excellent BioNumbers website will be helpful. Plot the respective dimensionless mRNA and protein concentrations over time. Comment on the nature of the responses of the unregulated versus regulated circuit. Which has a faster response? How long does it take each to get to steady state?
1.2: Autoactivation, bistability, and the importance of leakage, 30 pts¶
In this problem, we will explore a very simple circuit: autoactivation of a single gene, shown in the figure below. We will assume a separation of time scales in mRNA and protein degradation/dilution such that we only need to consider the dynamics of the protein, and we will call its concentration $x$. We will further assume that the autoactivation effect can be modeled as a Hill function with Hill coefficient $n$.
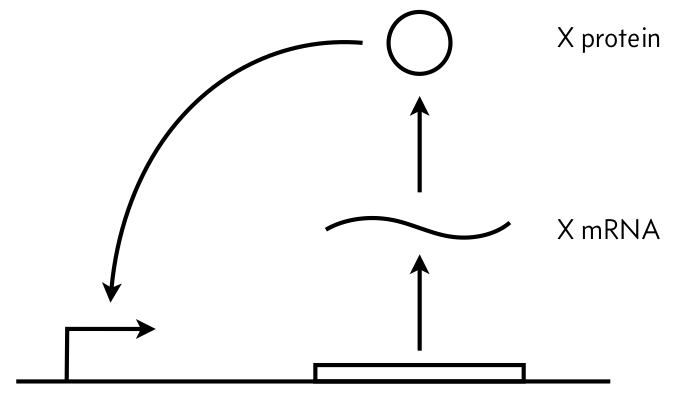
a) Write down an ODE describing the dynamics of $x$. Include leakage parametrized by $\alpha$.
b) Show that for $n = 1$, only one steady state exists for $\alpha > 0$. Show further that when $\alpha = 0$, two steady states may exist, but only one is stable.
c) In part (b), we considered the case where activation is not cooperative. We now consider the other extreme, where activation is infinitely cooperative. Derive the condition for bistability when $n\to\infty$. In other words, for what parameter values does the circuit exhibit two stable steady states? Discuss this condition as it relates to design principles for bistability.