Homework 4¶
(c) 2019 Justin Bois and Michael Elowitz. With the exception of pasted graphics, where the source is noted, this work is licensed under a Creative Commons Attribution License CC-BY 4.0. All code contained herein is licensed under an MIT license.
This document was prepared at Caltech with financial support from the Donna and Benjamin M. Rosen Bioengineering Center.

This homework was generated from a Jupyter notebook. You can download the notebook here.
4.1: Robustness to copy number, 30 pts¶
Segall-Shapiro, Sontag, and Voigt (Nat. Biotech., 2018) proposed a simple circuit that they claim can reduce the impact of changes in the copy number of a gene to the concentration of the gene product. The circuit consists of two genes, X and Y, with X being unregulated and Y being repressed by X. The production rate or X is proportional to its copy number, $c$. Segall-Shapiro and coworkers put Y very close to X in the genome, such that the unregulated production rate of Y is also proportional to $c$.
a) Write down a system of ODEs for the circuit and solve for the steady state concentration of Y.
b) Over what operating regime is the steady state concentration of Y robust to changes in copy number $c$?
c) Consider another simple circuit wherein Y is autorepressive (with the production rate still being proportional to $c$ in the $y\to 0$ limit). There is no X in this circuit. Over what operating regime is the steady state concentration of Y robust to changes in copy number $c$ in this circuit? How does this compare to the circuit proposed by Segall-Shapiro and coworkers?
4.2 The KaiABC clock, 70 pts¶
This problem was edited from a contribution from Joe Markson, based on his paper on the KaiABC clock (Science, 2007).
The KaiABC circuit is a protein-based circadian oscillator found in cyanobacteria. The main protein, KaiC, has two distinct phosphorylation sites. Therefore it has four possible states: unphosphorylated (U), phosphorylated at the threonine site (T), phosphorylated at the serine site (S), or phosphorylated at both sites (D).
a) Consider the following KaiC reaction scheme. At first glance, a system like this appears like it might be able to support self-sustaining oscillations:
i) Write down a three-dimensional system of differential equations describing this system, assuming that the total amount of KaiC, $C_{tot} = T + U + D + S$, is constant. I.e., write down a system of ODEs for $T$, $D$, and $S$. Assume that $C_{tot} = $3.4 µM and $k = 0.116\text{ h}^{-1}$.
ii) Show that there is a unique fixed point and solve for it.
iii) Determine the stability of the fixed point using linear stability analysis.
iv) Numerically solve for the dynamics of the system from three different initial conditions for a total time of 200 hours. Plot the resulting trajectories.
v) Plot the total phosphorylation of KaiC (T + D + S) versus time for each of the three initial conditions. Explain intuitively why the dynamics have this form, and why this scheme does not appear to generate self-sustaining oscillations. Would you expect the system to behave differently if there were only one molecule of KaiC?
b) Now consider the same system with feedback mediated by KaiA and KaiB.
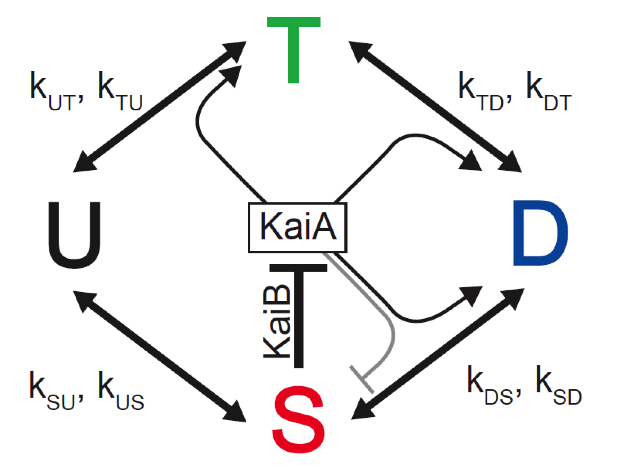
We define $k_{XY}$ as the mass action rate constant (which depends indirectly on S and on the concentration of KaiA, $A$) for the conversion from phosphoform X to phosphoform Y. E.g., the rate of conversation from D to S is $k_{DS} D$. We take these constants to be of the following form.
\begin{align} k_{XY} &= k^{\text{basal}}_{XY} + k^A_{XY}\,\frac{A_\mathrm{act}}{A_\mathrm{act}+K_{1/2}}, \end{align}where
\begin{align} A_\mathrm{act} &= \text{max}\{ 0, A_\mathrm{tot}-2S \} . \end{align}The constants $C_\mathrm{tot}$, $A_\mathrm{act}$, $k^{\text{basal}}_{XY}$, $k^A_{XY}$, and $K_{1/2}$ are given in the following table.
| Parameter | Value | Units |
|---|---|---|
| $k^{\text{basal}}_{UT}$ | 0 | - |
| $k^{\text{basal}}_{TD}$ | 0 | - |
| $k^{\text{basal}}_{SD}$ | 0 | - |
| $k^{\text{basal}}_{US}$ | 0 | - |
| $k^{\text{basal}}_{TU}$ | 0.21 | h$^{-1}$ |
| $k^{\text{basal}}_{DT}$ | 0 | - |
| $k^{\text{basal}}_{DS}$ | 0.31 | h$^{-1}$ |
| $k^{\text{basal}}_{SU}$ | 0.11 | h$^{-1}$ |
| $k^{\text{max}}_{UT}$ | 0.479077 | h$^{-1}$ |
| $k^{\text{max}}_{TD}$ | 0.212923 | h$^{-1}$ |
| $k^{\text{max}}_{SD}$ | 0.505692 | h$^{-1}$ |
| $k^{\text{max}}_{US}$ | 0.0532308 | h$^{-1}$ |
| $k^{\text{max}}_{TU}$ | 0.0798462 | h$^{-1}$ |
| $k^{\text{max}}_{DT}$ | 0.173 | h$^{-1}$ |
| $k^{\text{max}}_{DS}$ | -0.319385 | h$^{-1}$ |
| $k^{\text{max}}_{SU}$ | -0.133077 | h$^{-1}$ |
| $K_{1/2}$ | 0.43 | µM |
| $A_\mathrm{tot}$ | 1.3 | µM |
| $C_\mathrm{tot}$ | 3.4 | µM |
i) Write down a the system of ODEs describing this system. Numerically solve them for three different initial conditions of your choosing and plot the result. Make sure that your initial conditions $(T_0, D_0, S_0)$ respect the fact that $T_0 + D_0 + S_0 \leq C_{tot}$. Make sure you integrate long enough to observe the dynamics (200 hours for dimensional units should work).
ii) Plot total concentration of phosphorylated KaiC ($T + D + S$) versus time for each of the three initial conditions.
iii) What is the period of the oscillator? Does it depend on the initial conditions? Why or why not?
iv) Why do the initial (transient) dynamics differ depending on initial conditions?
c) A key characteristic of circadian clocks is their so-called phase response curve (PRC), which describes how the phase of the clock changes in response to a stimulus/perturbation such as exposure to light for a defined duration. A PRC is a plot of the change in phase of the clock ($y$-axis) versus the phase (subjective time) at which the perturbation is applied ($x$-axis). The phase change is evaluated by comparing the phase of the perturbed clock to the phase expected in the absence of perturbation several periods after the perturbation to allow the phase of the perturbed clock to stabilize.
i) For the KaiABC system with feedbacks, apply a perturbation described by
\begin{align} \delta = (\delta T, \delta D, \delta S) = (-0.05 \mu M, -0.05 \mu M, -0.05 \mu M) \end{align}at each hour of the day, that is for 24 different times evenly spaced within [103.5 h, 103.5 hours $+ T$), where $T$ is the period you determined in 3b(iii). (Note that a given system is perturbed only once; you need to run 24 different simulations.) Calculate the trajectories of each of the perturbed systems for at least six periods following the perturbation. Also, calculate the trajectory of an unperturbed clock for at least seven periods following 103.5 hours. Plot the total phosphorylation for the 1st, 6th, 12th, and 18th perturbations versus time, for $t = [100, 200]$. On the same plot, show the total phosphorylation of the unperturbed clock over the same time period.
ii) Now calculate and plot the phase response curve for those 24 perturbations. Define the time at which the perturbation is applied as $24\times (t_\mathrm{perturb}-t_\text{preceding peak})/T$. Here, $t_\mathrm{perturb}$ is the time at which the perturbation is applied, $t_\text{preceding peak}$ is the time of the last peak of total phosphorylation immediately preceding $t_{perturb}$, and $T$ is the period of the oscillator. The time should lie in the interval [0 h, 24 h). (This formula normalizes time to that of an idealized 24-hour clock, resulting in a measure called circadian time [CT], which is standard in the field.) Define the phase change after perturbation, measured in the CT shift of the total phosphorylation peak, such that it lies in the interval [-12 h, +12 h). To determine the phase change, consider the phase of the perturbed oscillator beginning $5T$ after perturbation compared to that of the unperturbed oscillator. Match the trajectories plotted in 3c(i) to their circadian times.
iii) Describe the implications of this PRC for you if you were a cyanobacterium traveling from Los Angeles to Beijing via a Star Trek-style (instantaneous) transporter. The time in Beijing is 15 hours ahead of the time in Los Angeles; in the date-agnostic PRC in 3c(ii), in which phase changes lie in [-12 h, 12 h), this time difference would be equivalent to a 9-hour phase delay (-9 h). If you could perturb your clock with perturbation $\delta$ once per day, and the phase change were instantaneous (for the sake of simplicity), describe a scheme for synchronizing your circadian clock with Beijing time.