Homework 7¶
(c) 2019 Justin Bois and Michael Elowitz. With the exception of pasted graphics, where the source is noted, this work is licensed under a Creative Commons Attribution License CC-BY 4.0. All code contained herein is licensed under an MIT license.
This document was prepared at Caltech with financial support from the Donna and Benjamin M. Rosen Bioengineering Center.

This homework was generated from a Jupyter notebook. You can download the notebook here.
7.1: Ruling out oscillations, 30 pts¶
This problem is based on problem 3.6 of Del Vecchio and Murray.
There are fifteen circuits in the figure below. Use the Bendixson criterion to identify circuits that cannot give sustained oscillations.
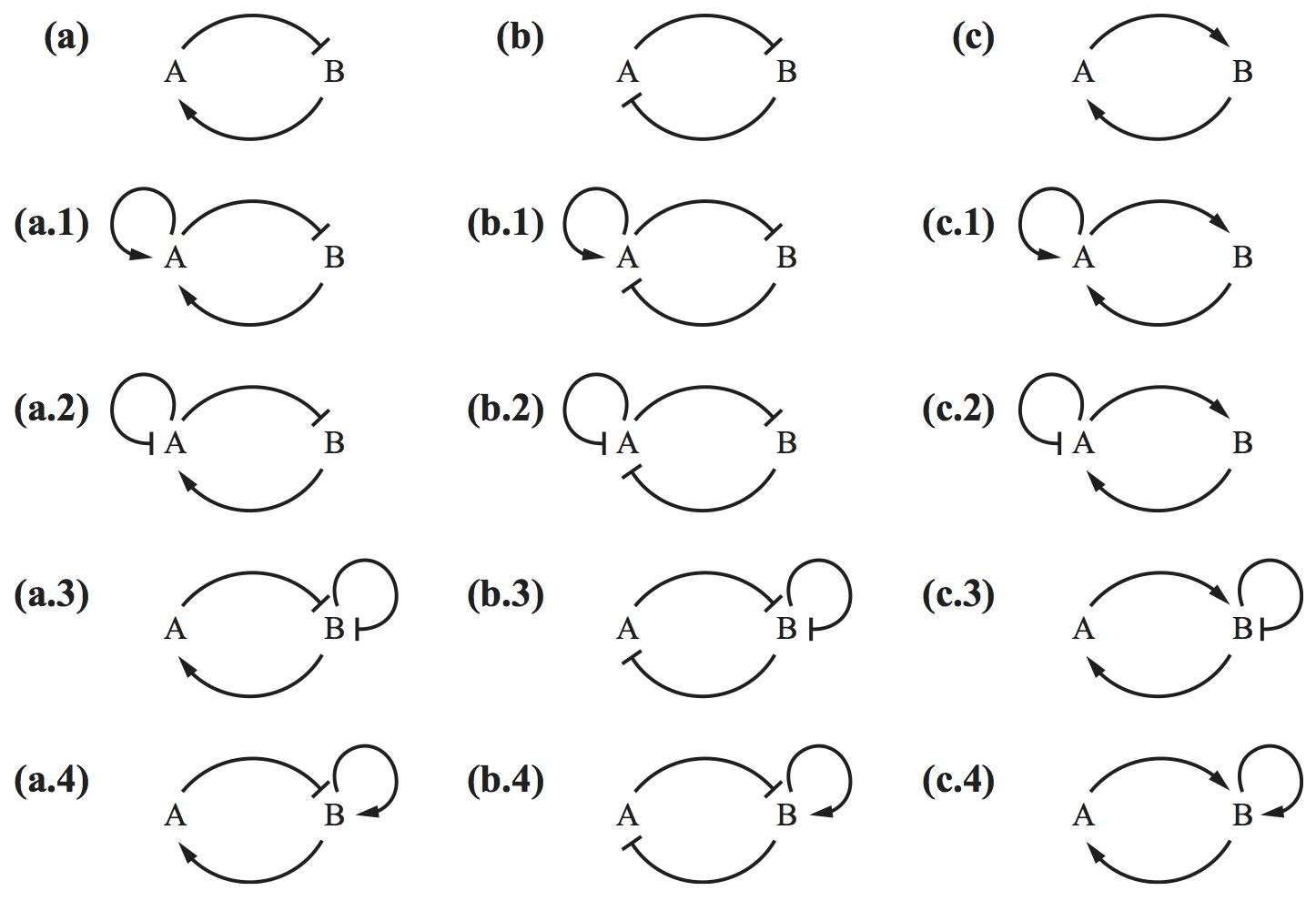
7.2: The activator-repressor clock, 35 pts¶
You should have found that circuit a.4 above is not precluded from periodic solutions by the Bendixson criterion. We will now analyze this circuit.
Assume that the regulation of B follows AND logic. Assume further that there is possibly leakage for both A and B.
a) Write a system of dimensionless ODEs to describe the dynamics of this system. Then use the Bendixson criterion to constrain which parameter values enable oscillations.
b) For a set of parameter values that do give sustained oscillations construct a phase portrait, including nullclines and the fixed point(s). Also add a few trajectories to the phase portrait to display the limit cycle.
c) Can this circuit also oscillate if A is also autorepressive? Support your answer with an analysis.
7.3: Dynamics of a chemostat, 35 pts¶
During Roy Kishony's guest lecture, we heard about his invention, the morbidostat, in which we could control levels of antibiotic concentrations to regulate cellular growth rate. A similar invention is a chemostat. Here, a solution of bacteria in medium is held in a well-mixed, well-aerated vessel with a total solution volume $V$. There is an inflow of sterile medium that has necessary nutrients for the bacteria to grow. To maintain the constant volume, there is an equal outflow of the bacterial medium. The outflowing medium contains depleted nutrients, living and dead bacteria, and waste.
Let $Q$ be the volumetic inflow rate of fresh medium (and also the outflow rate). Let $c$ be the concentration of living bacterial cells in the vessel and let $n$ be the concentration of nutrient in the vessel. We denote by $n_0$ the concentration of nutrients in the incoming fresh medium.
a) Explain why the following equation is a reasonable model for bacterial concentration.
\begin{align} \frac{\mathrm{d}c}{\mathrm{d}t} = \beta\,\frac{n/k}{1 + n/k}\,c - \frac{Q}{V}\,c. \end{align}b) Taking the above equation as given, and defining by $\nu$ the number of nutrient molecules needed to make one bacterium, derive an expression for $\mathrm{d}n/\mathrm{d}t$.
c) Nondimensionalize your equations. You should end up with two dimensionless parameters. One is a dimensionless version of the inlet nutrient concentration and the other is a dimensionless growth rate.
d) Analyze the circuit. Include at least the following in your analysis:
- The number of fixed points for various parameter values.
- Phase portraits with nullclines and fixed points.
Based on your analysis, propose an inlet flow rate that will ensure a stable bacterial population.