Homework 3.1: Co-substrate compensation (50 pts)¶
This problem derived from discussions with H. Y. Kueh, and is based on his paper (Biophys J., 104, 1338–1348, 2013).
To put this problem in context, let us think about an intriguing question. Oxygen is delivered to the cells of your body through your blood. Naturally, cells are situated at difference distances from blood vessels. As oxygen diffuses away from the blood vessels, different cells experience different local oxygen concentrations, often very different concentrations. How, then, do cells respire at the same rate, despite the large difference in oxygen concentration?
This is a question of robustness. Is rate of respiration robust to differences in oxygen concentration over a physiologically relevant operating regime? To address this question consider a simple model of the mitochondrial electron transport chain (ETC) consisting of a single electron carrier C and two reactions that catalyze its oxidation and reduction, shown in below.
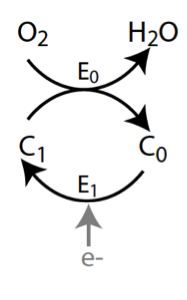
The carrier can exist in an oxidized state C₀ and in a reduced state C₁. The oxidation reaction is catalyzed by enzyme E₀, and the reduction reaction is catalyzed by enzyme E₁.
a) In this part of the problem and in part (b), we will write down governing ODEs for the dynamics of this system. We will do so by first splitting the system into its two enzyme-catalyzed reactions. We start with the lower one. We can write the reaction as
C₀ + E₁ ⇌ C₀·E₁ ⟶ C₁ + E₁.
We will assume Michaelis-Menten kinetics (and the assumptions involved therein). First, write an expression for the rate of electron transfer, which is the rate of production of reduced substrate C₁, \(v_1\). Note that
\begin{align} v_1 = \frac{\mathrm{d}c_1}{\mathrm{d}t}\;\text{considering only the bottom reaction}, \end{align}
where \(c_1\) is the concentration of C₁. Of course, the complete expression for \(\mathrm{d}c_1/\mathrm{d}t\) arises from both the top and bottom reactions. Then, assume that the ratio of the concentration of C₀ to its Michaelis constant is much smaller than one. Show that we can then write
\begin{align} v_1 = k_1\,c_0, \end{align}
where various constants have been absorbed into \(k_1\).
We will now write down the rate of oxidation of C₁, which we will call \(v_0\). Analogously to what we have done so far,
\begin{align} v_0 = \frac{\mathrm{d}c_0}{\mathrm{d}t}\;\text{considering only the top reaction}, \end{align}
where \(c_0\) is the concentration of C₀. This is the quantity we are most interested in; it is the rate of oxygen consumption. We can describe this reaction as follows. The substrate C₁ cannot bind oxygen unless complexed with the enzyme E₀, to which is binds reversibly. The C₁·E₀ complex can them reversibly bind oxygen. Finally, the C₁·E₀·O₂ complex gets irreversibly converted to oxidized substrate C₀, freeing the enzyme E₀ and producing water in the process. We can write these steps as follows.
C₁ + E₀ ⇌ C₁·E₀
C₁·E₀ + O₂ ⇌ C₁·E₀·O₂
C₁·E₀·O₂ ⟶ C₀ + E₀ + H₂O
If we write down the expressions for mass action kinetics and apply a quasi-steady state approximation such that the concentrations of C₁·E₀ and C₁·E₀·O₂ do not change appreciably, we can derive
\begin{align} v_0 = k_0 \, c_1\,\frac{c_{\mathrm{O}_2}/K_0}{1 + c_{\mathrm{O}_2}/K_0}, \end{align}
where \(c_{\mathrm{O}_2}\) is the oxygen concentration and \(k_0\) and \(K_0\) are positive constants. You may derive this relation if you like, but you are not required to.
b) Assume that the amount of substrate that is bound to enzyme is negligible compared to that which is unbound. That is, the concentration of C₀ plus that of C₁ is much greater than the sum of the concentrations of all enzyme bound substrate. Thus, the total substrate concentration, \(c_t \approx c_0 + c_1\) is constant.
Given the expressions from part (a), derive a differential equation for the dynamics of \(c_1\). Specifically, write an expression for \(\mathrm{d}c_1/\mathrm{d}t\) in terms of constants given in the expressions for \(v_0\) and \(v_1\), as well as the oxygen concentration \(c_{\mathrm{O}_2}\), the constant total substrate concentration \(c_t\), and \(c_1\).
c) Write down an expression for the rate of oxygen consumption, \(v_0\), at steady state.
d) In what operating regime is the steady state oxygen consumption rate independent of oxygen concentration? On other words, what parameter values ensure robustness in the oxygen consumption rate?
e) You have shown that for some operating regime, the rate of oxygen consumption is robust to variation of oxygen concentration. Now imagine that the system is in steady state and there is a sudden step in oxygen concentration. In looking at your differential equation in part (b), you should be able to identify the time scale for recovery to steady state consumption rate. Is the time to recovery robust to variations in oxygen concentration? If so, over what operating regime?
f) Define the oxygen concentration for which the steady state oxygen consumption rate is half-maximal as \(K_\mathrm{m}\). The Chance relationship Chance, J. Gen. Physiol., 1965 says that \(K_m\) scales linearly with the maximal rate of electron transfer (the maximal \(v_1\)), and inversely with the reaction rate constant for oxygen reduction (\(k_0\)). In the regime where oxygen consumption rate is independent of oxygen concentration, does this system satisfy the Chance relation?