Homework 5.1: Ruling out oscillations (30 pts)

This problem is based on problem 3.6 ofDel Vecchio and Murray.

---

An important result from dynamical systems known as the Bendixon criterion makes it possible to rule out sustained oscillations (defined as orbits, closed curves in the phase plane on which trajectories remain after entering).

Consider a dynamical system

\begin{align} &\frac{\mathrm{d}x}{\mathrm{d}t} = f(x, y)\\[1em] &\frac{\mathrm{d}y}{\mathrm{d}t} = g(x,y). \end{align}

In a simply connected region \(D\) of the \(x\)-\(y\) plane, if the quantity

\begin{align} \frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} \end{align}

is nonzero and does not change sign on \(D\), then the dynamical system has no orbits entirely in \(D\). To illustrate the power of this, I really like the following exercise from Del Vecchio and Murray’s book in which they ask you to eliminate circuits below that cannot have sustained oscillations by using Bendixson’s criterion. (Image below, (c) Princeton University Press.)

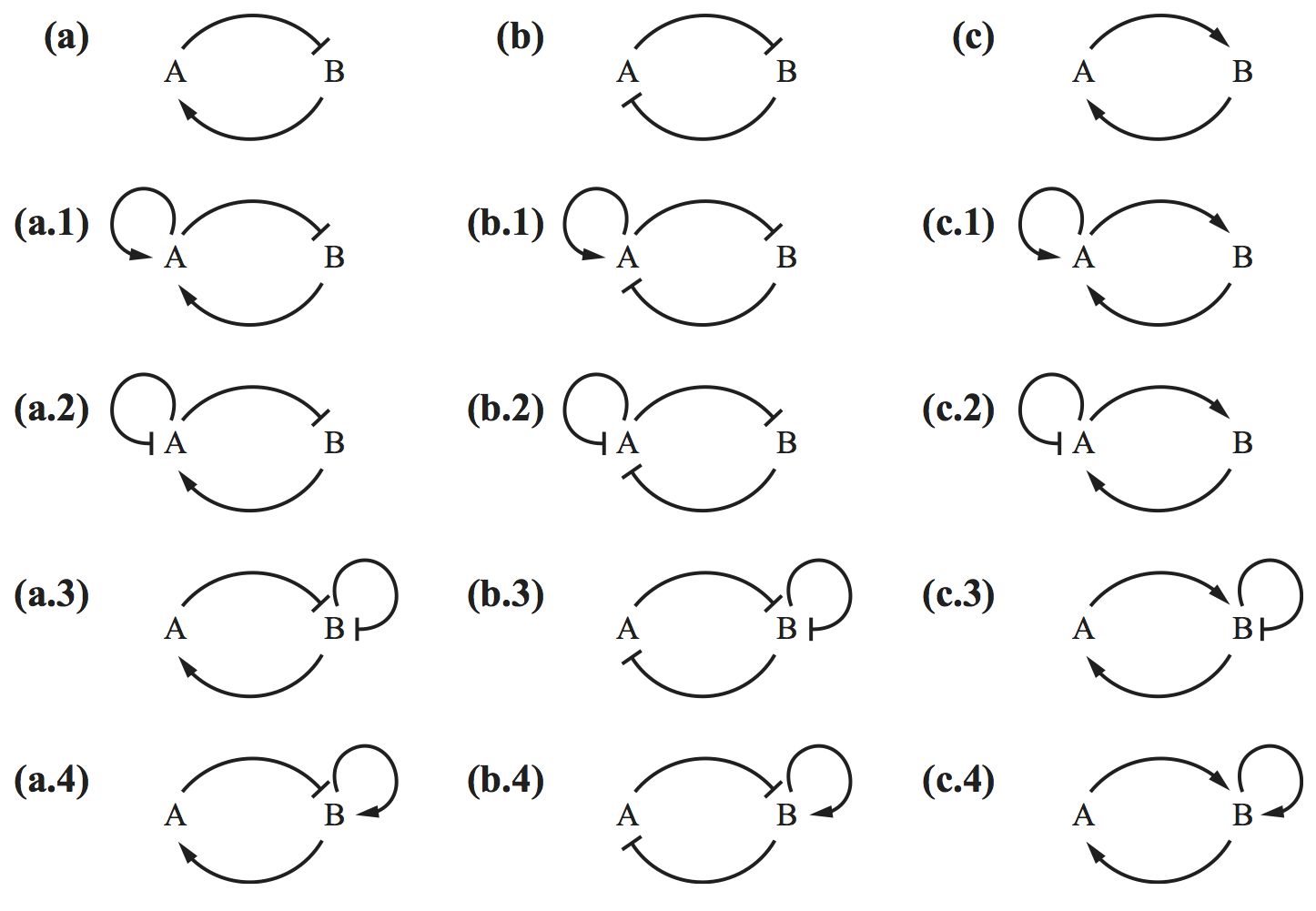
Identify the circuits that cannot have sustained oscillations by Bendixson’s criterion.